Experiment 5 User Defined Function Bessel Function ( Series Expansion )
User Defined Function Bessel Function ( Series Expansion )
The Bessel functions have been known since the 18th century when mathematicians and scientists started to describe physical processes through differential equations. Many different looking processes satisfy the same partial differential equations. These equations were named Laplace, d‘Alembert (wave), Poisson, Helmholtz, and heat (diffusion) equations. Different methods were used to investigate these equations. The most powerful was the separation of variables method, which in polar coordinates often leads to ordinary differential equations of special structure:
x^2*y" + xy' + (x^2 − n^2 )y = 0
where n is an integer or a half-integer.
CONCEPT
(a)(Bessel Differential Equation)
The Bessel differential equation is
x^2*y" + xy' + (x^2 − n^2 )y = 0
where n is an integer or a half integer.
(b) (Bessel Function) The series solution Jn(x) to this equation
METHOD/CODE
(a)(Factorial Function) The Gamma function Γ(n) or the factorial n! = Γ(n + 1) (when n is a positive integer) follow the recursive relation
Γ(n + 1) = nΓ(n) or (n + 1)! = (n + 1)n!
Write a code to generate the Gamma function Γ(n) for an arbitrary n.
(b) (Bessel Function) Write a code to generate the Bessel function as sum of finite number of terms of the series expansion.
(c) (Derivative of Bessel Function) Write a code to generate the derivative of Bessel function as sum of finite number of terms of the series expansion.
APPLICATIONS
(a) (Bessel Polynomial) Generate the values of J0(x), J1/2(x) and J1(x) Bessel polynomials in the range [0, 20] using explicit series representation taking 100 data points of x within the given range. Store them in tabulated form as x, J0(x), J1/2(x) and J1(x) in the data file bes01.dat. Retrieve these values and plot these functions. Display the same on the console.
(b) (Derivative of the Bessel Polynomial) Generate the values of derivative J 0 0 (x) of the Bessel polynomial J0(x) in the range [0, 20] using explicit series representation taking 100 data points of x within the given range. Append the same in the data file bes01.dat. Retrieve these values and plot J 0 0 (x) along with J1(x). Display the same on the console.
SCILAB CODE FOR THE GIVEN PROBLEM :
clc,clear
clf
//********************
//User Defined Function
//Bessel Function ( Series Expansion )
//********************
function f=fact(n) //(Factorial Function)
if n==int(n)
f=1
for i=1:n
f=f*i
end
else
f=sqrt(%pi)
for i=(1/2):(n-1)
f=f*i
end
end
endfunction
function g=gama(n) //(gamma function)
if n==int(n)
g=fact(n-1)
else
g=fact(n)
end
endfunction
for n=1:1/2:2
for x=1:0.2:21
j=0
dJ=0
for i=1:100
j=j+((((-1)^(i-1))*((x-1)^((n-1)+2*(i-1))))/((fact(i-1))*(gama(n+i-1))*(2^((n-1)+2 *(i-1))))) // (Bessel Function)
dJ=dJ+(((-1)^(i)*(n-1+2*i)*(x-1)^(n-1+2*i-1)))/(fact(i)*gama(n+i)*2^(n-1+2*i)) //(Derivative of Bessel Function)
end
disp([n-1 x-1 j dJ])
if n==1
plot(x-1,j,".m",x-1,dJ,".k")
legend("j","diff J")
else
if n==2
plot(x-1,j,".r",x-1,dJ,".b")
legend("j","diff J")
else
if n==1.5
plot(x-1,j,".b",x-1,dJ,".y")
legend("j","diff J")
xgrid(5, 1, 7)
xtitle('Bessel Functions of the first kind')
end
end
end
end
end
p=besselj(0.5,20)
disp(p,"Calculated value is(0.5): ")
q=besselj(0,20)
disp(q,"Calculated value is(0): ")
r=besselj(1,20)
disp(r,"Calculated value is(1): ")
************************************
Calculated value is(0):
0.1670247
//20. 0.1670247 -0.0668331
Calculated value is(0.5):
0.1628808
//20. 0.1628808 -0.0204713
Calculated value is(1):
0.0668331
//20. 0.0668331 -0.336317
Make Adjustment according to Your Given Problem .
NOTE :- If you have any Problem or Query Regarding this Blog Please Comment Down Or Reach us Out at scilabprogram@gmail.com
//university of Delhi //Department of Physics
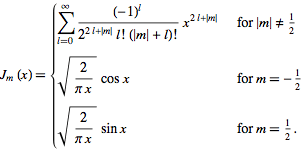
Comments
Post a Comment